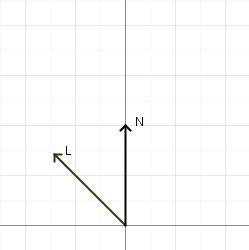
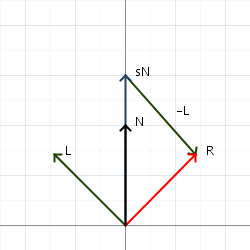
I’ve been spending quite a bit of time learning shaders and with that, learning SDFs (Signed Distance Functions). SDFs are very useful for rendering geometric shapes. There’s certainly a beauty to them–composed basically of just a bunch of math. Often void conditionals, they are efficient, but not so readable.
When first learning to read SDFs, it can be daunting. Just take a look at the definition for a cylinder:
float sdCylinder(vec3 p, vec2 sz ){
vec2 d = abs(vec2(length(p.xz),p.y)) - sz;
float _out = length(max(vec2(d.x,d.y), 0.));
float _in = min(max(d.x,d.y), 0.);
return _in + _out;
}
Errr, what? A month ago, I would have given up after the second line. Certain visualization tools are necessary to help break apart the logic, which is what this blog is all about.
Anyway, this week I was in process of understanding a cylinder SDF and I had a neat insight. Understanding the logic is much easier if visualized with flies and force fields.
Game Rules
In this world, our object is enveloped in force fields. Each field has a fly trapped inside. Poor dudes. Flies cannot pass between the fields. There’s the “tube” force field that defines the radius of the cylinder and force fields along the XZ-planes controlling the height.
There’s also a fly trapped inside the object itself and another stuck directly on the cylinder. Other than not being able to pass between fields, the flies (our sample points) are free to travel anywhere inside the field. And each case, there is a straight-line distance from the fly/point to the object. The force fields represent the different cases of our logic. Hmmm, a diagram might help:
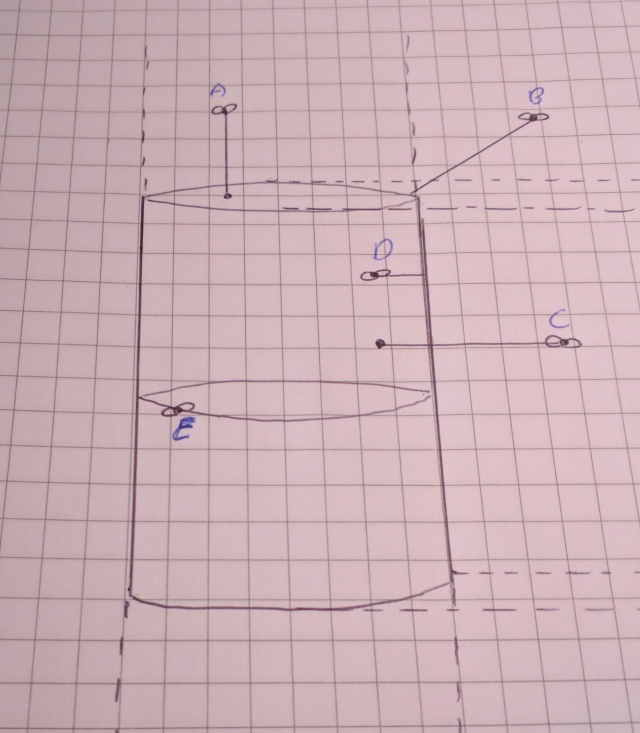
If you spend a bit of time visualizing each case separately, seeing the flies buzzing in their respective fields, it becomes more clear how the different parts of the logic work.
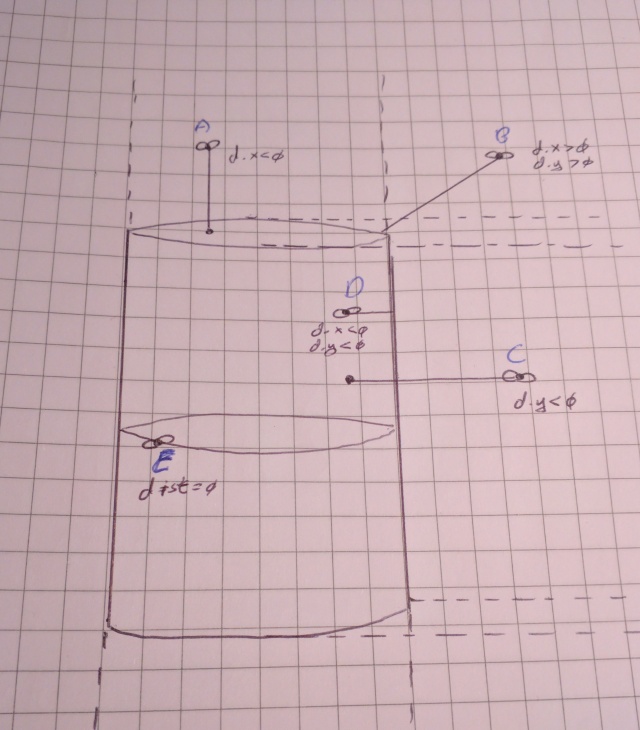
Fly A: (y – height) => (Cylinder Top)
Fly B: length of vec2(p.xz – radius, p.y – height) => (Cylinder Rim)
Fly C: length of (p.xz – radius) => (Cylinder Body)
Fly D: greater of length of (p.xz – radius) OR (y-height) => (Inside Cylinder)
Fly E: distance = zero, strictly lives on cylinder
Okay, let’s dive in.
float sdCylinder(vec3 p, vec2 sz ){
Easy stuff here. Return a float since which is our distance from the sample point to the surface of the object. The two parameters are a vec3 p and a vec2 sz. The sz variable contains the radius and height of the cylinder as its x and y components respectively.
vec2 d = abs(vec2(length(p.xz),p.y)) - sz;
The vec2 defined contains p.xz distance from the origin and p.y. We use abs since a cylinder is symmetrical and only the “top right front” part needs to be evaluated. Everything else is just a “mirror” case. Subtracting sz yields the differences for both the “top” and “body” distances. Store that in d.
float _out = length(max(vec2(d.x, d.y), 0.));
Using max with zero isolates which case we’re working with. If the point/fly is at the top of the cylinder, then d.x < 0. If it is in the ‘body’ force field, it’s d.y 0 and d.y > 0, the we’re dealing with fly B. The neat part is that either we’ll have one component set to zero in which case length is just using 1-dimensions, or we’ll have 2 components, which case length still works.
float _in = min(max(d.x,d.y), 0.);
Lastly, if the fly is trapped inside, then which surface is it closer to? Top or body? d.y or d.x? Use max to find that out. If one of the values are positive here, min is used to set it to zero. Think of min here as a replacement to a conditional.
Again, here is the final definition:
float sdCylinder(vec3 p, vec2 sz ){
vec2 d = abs(vec2(length(p.xz),p.y)) - sz;
float _out = length(max(vec2(d.x,d.y), 0.));
float _in = min(max(d.x,d.y), 0.);
return _in + _out;
}
This visualization tool has helped me to deconstruct the SDF logic. I hope it has been of use to you too! I suggest memorizing the five cases where the fly/point can exist. Then you can derive the code from scratch if necessary–it’s a good way of testing your understanding. It’s also really fun once you grasp it!